728x90
*[종속 변수]와 [독립 변수]?
예를 들어서 주택 가격을 예측하는 문제를 생각해 보면,
- 종속 변수: 주택 가격
주택 가격은 예측하고자 하는 대상이다.
- 독립 변수: 주택의 크기, 위치, 방의 개수, 욕실의 개수 등
주택 가격은 다양한 요소에 영향을 받을 수 있다. 주택의 크기, 위치, 방의 개수, 욕실의 개수 등은 독립 변수로서 주택 가격을 예측하기 위해 사용되는 변수들이다. 이러한 독립 변수들은 주택 가격에 영향을 미치는 요인들로서, 각 변수들의 값에 따라 주택 가격이 달라질 수 있다.
따라서, 주택 가격을 예측하기 위한 모델을 구축할 때에는 독립 변수인 주택의 크기, 위치, 방의 개수, 욕실의 개수 등을 입력으로 사용하여 종속 변수인 주택 가격을 예측하게 된다.
독립 변수의 변화에 따라 종속 변수인 주택 가격이 변화하게 된다.
- 종속 변수 유형:
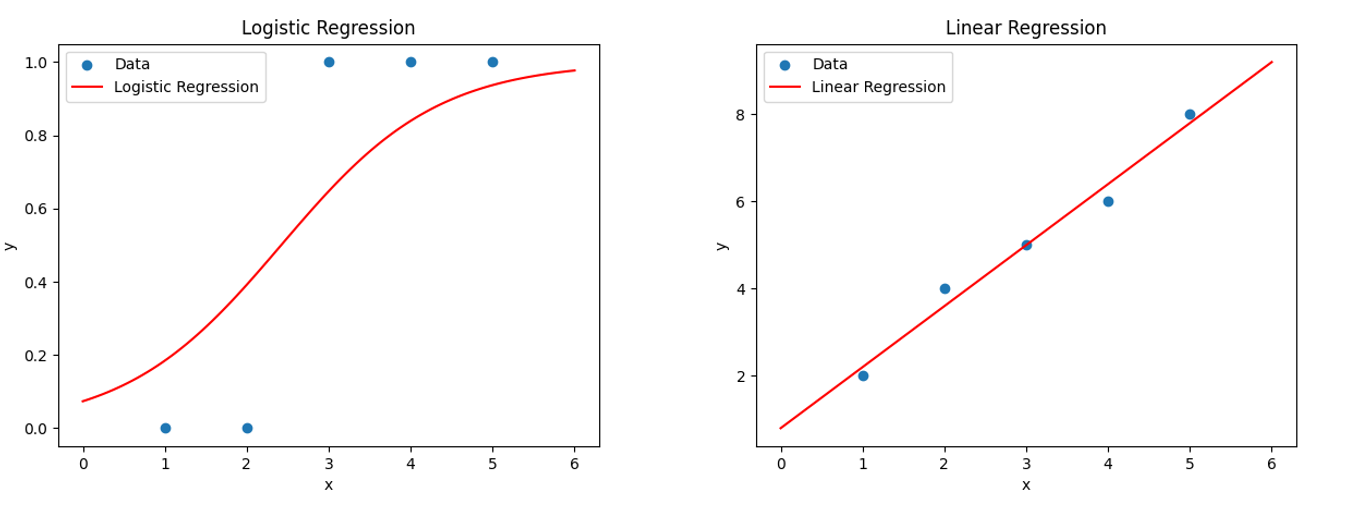
로지스틱 회귀는 이항 분류 문제(두 개의 클래스 중 하나를 예측) 또는 다항 분류 문제(세 개 이상의 클래스 중 하나를 예측)에 사용되는 반면,
선형 회귀는 연속형 숫자 값을 예측하는 문제에 사용된다. - 출력 값의 범위:
로지스틱 회귀의 출력은 0과 1 사이의 확률 값인 반면,
선형 회귀의 출력은 입력 변수에 선형적으로 의존하므로 임의의 실수 값을 가질 수 있다. - 가정:
로지스틱 회귀는 로짓 함수(logistic function)를 사용하여 종속 변수와 독립 변수 간의 비선형 관계를 모델링한다.
선형 회귀는 종속 변수와 독립 변수 간에 선형 관계를 가정한다. - 오차 함수:
로지스틱 회귀는 일반적으로 최대 로그 우도(Maximum Likelihood Estimation, MLE)를 사용하여 모델을 피팅시킨다.
이에 비해 선형 회귀는 주로 잔차 제곱합(RSS, Residual Sum of Squares)을 최소화하는 최소 제곱법(Ordinary Least Squares, OLS)을 사용한다. - 모델 해석: 로지스틱 회귀는 각 독립 변수의 계수를 통해 종속 변수에 대한 영향력을 해석할 수 있다. 계수의 부호와 크기는 해당 변수의 영향력을 나타낸다.
반면 선형 회귀에서는 독립 변수의 계수는 해당 변수가 종속 변수에 선형적으로 어떤 영향을 미치는지를 나타낸다.
요약하자면,
로지스틱 회귀는 분류 문제에 사용되는 모델로서 이항 분류나 다항 분류에 적합하며, 출력은 0과 1 사이의 확률 값이다.
선형 회귀는 연속형 숫자 값을 예측하는 회귀 문제에 사용되는 모델로서 출력은 임의의 실수 값이다.
728x90
'AI' 카테고리의 다른 글
| 다중 선형 회귀(Multiple Linear Regression) VS. 다항 회귀(Polynomial Regression) (0) | 2023.06.30 |
|---|---|
| 데이터를 train, valid, test로 나누는 이유는? (0) | 2023.06.30 |
| 나이(Age)의 데이터 형태는 범주형인가, 수치형인가? (0) | 2023.05.20 |
| 로지스틱 회귀(Logistic Regression) (0) | 2023.04.25 |
| 정보 이론 (0) | 2023.04.25 |