728x90
파이썬 코드로 딥러닝을 위한 수학적인 공식들이 어떻게 나타나는지 알아보자.
import math
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
일차함수(Linear Function)
- y = ax+b, a: 기울기, b: y절편
- 직선으로 나타난다.
def linear_function(x):
a = 0.8 #기울기
b = 2 # y절편은 고정값
return a * x + b- x가 5일 때 y는 6
print(linear_function(5))>> 6.0
- -5부터 5까지 0.1씩 배열 만들기
np.arange(-5,5,0.1)>>

- x축의 값으로 저장한다
x = np.arange(-5,5,0.1)
y = linear_function(x)
print(y)>>

- 시각화 하기
plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Linear Function')>> Text(0.5, 1.0, 'Linear Function')

이차함수(Quadratic Function)
- y=ax^2+bx+c
- 보통 두 개의 실근을 가진다.
def quadratic_function(x):
a = 1
b = -1
c = -2
return a*x**2 + b*x + c- x=2일 때, y=0
print(quadratic_function(2))>> 0
- 시각화 하기
y = quadratic_function(x)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Quadratic Function')>> Text(0.5, 1.0, 'Quadratic Function')

삼차함수(다항함수, Cubic Function)
- y=ax^3+bx^2+cx+d
def cubic_function(x):
a = 4
b = 0
c = -1
d = -8
return a*x**3 + b*x**2 + c*x+d- 시각화 하기
y = cubic_function(x)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Quadratic Function')>> Text(0.5, 1.0, 'Quadratic Function')

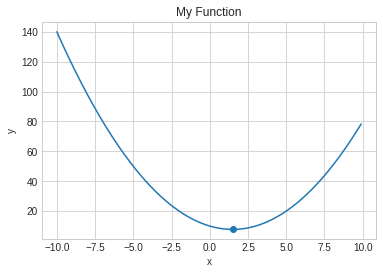
- 최소값, 최대값 구하기
- 전체 데이터를 모를 때는 하강법을 사용할 수 있다.
def my_func(x):
a = 1
b = -3
c = 10
return a*x**2 + b*x + c
- -10부터 10까지 0.1씩 커지는 배열을 만든다.
x = np.arange(-10, 10, 0.1)
y = my_func(x)- 시각화 하기
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('My Function')*점을 찍어보기
plt.scatter(1.5, my_func(1.5))>>
지수함수/로그함수(Exponential Function)
- 지수함수-로그함수는 역함수 관계(y=x 직선 대칭, 단 밑이 같을 때)
- y=ax
def exponential_function(x):
a = 4
return a**x- x=4, x=0 값을 줘 본다.
>>
256
1
- -3부터 2까지 0.1씩 커지는 배열을 만든다.
x = np.arange(-3, 2, 0.1)
y = exponential_function(x)- 시각화 하기
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(-4, 3)
plt.ylim(-1, 15)
plt.title('exponential_function')>>
Text(0.5, 1.0, 'exponential_function')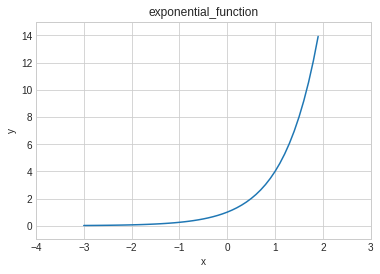

728x90
'MS AI School' 카테고리의 다른 글
| Day 26 - 신경망 구조(퍼셉트론, 논리회로, 활성화 함수) (0) | 2022.11.29 |
|---|---|
| Day 25 - 신경망 데이터(텐서, 1차원, 2차원, 3차원..) (0) | 2022.11.29 |
| DAY 23 - 딥러닝 이론 (0) | 2022.11.26 |
| DAY 22 - 머신러닝 비지도 학습: 클러스터링(Clustering) (0) | 2022.11.23 |
| DAY 21 - 머신러닝 지도 학습: 분류(Classification) (0) | 2022.11.23 |