머신러닝에서 사람이 직접 가중치 조절을 하는 반면, 딥러닝에서는 컴퓨터가 가중치 조절을 한다.
그렇다면 딥러닝을 위해 사람이 해야 할 일은 무엇일까?
바로 문제에 맞는 신경망 구성과 신경망을 돌릴 수 있는 강력한 high quaility의 컴퓨터를 준비하는 것이다.
Money 또한 실력의 일부!!

뉴런의 수학적 표현 - 활성화 함수(Activation Function)
활성화 함수(Activation function)란 입력된 데이터의 가중 합을 출력 신호로 변환하는 함수이다. 인공 신경망에서 이전 레이어에 대한 가중 합의 크기에 따라 활성 여부가 결정된다. 신경망의 목적에 따라, 혹은 레이어의 역할에 따라 선택적으로 적용한다.


- f: 활성화 함수. 임계값을 경계로 출력이 바뀐다.
- b: bias. 편향값으로 결정 경계선을 원점에서부터 벗어나게 한다. 노드의 민감도나 활성화를 조정하여 만족스러운 모델을 fit하기 위함
- i: input의 계수
완전 연결 계층(Fully-Connected Layer)의 수학적 표현
뉴런이 모인 한 단위를 계층(Layer)라고 하며, 모든 뉴런이 서로 연결된 계층을 Fully-Connected Layer(dense layer)라고 한다.


논리회로
- 논리 게이트(Logic Gate)
AND

Input(A, B) → Output(Y)
0, 0 → 0
1, 0 → 0
0, 1 → 0
1, 1 → 1
: 두 입력이 모두 1인 경우에만 출력이 1이 되고, 그 외의 경우에는 출력이 0이 된다.
NAND

Input(A, B) → Output(Y)
0, 0 → 1
1, 0 → 1
0, 1 → 1
1, 1 → 0
: NOT AND의 약자로, AND 게이트의 출력을 반대로 만들어준다.
OR

Input(A, B) → Output(Y)
0, 0 → 0
1, 0 → 1
0, 1 → 1
1, 1 → 1
: 두 입력 중 하나라도 1이면 출력이 1, 두 입력 모두 0일 경우에만 0이 출력된다.
NOR

Input(A, B) → Output(Y)
0, 0 → 1
1, 0 → 0
0, 1 → 0
1, 1 → 0
: OR 게이트의 출력을 반대로 만들어준다.
두 개의 입력을 받으며 , 입력이 모두 0일 경우에만 출력이 1이 되고 그 외의 경우에는 출력이 0이 된다.
NOT

Input(A) → Output(Y)
0 → 1
1 → 0
: 입력이 1이면 출력은 0, 입력이 0이면 출력은 1이 된다.
XOR

: 배타적 논리합(Exclusive OR)의 약자로, 두 입력이 같으면 0이 출력된고 다르면 1이 출력된다.
파이썬 코드로 구현해 보기
import numpy as np
import matplotlib.pyplot as plt
- AND 게이트
def AND(a, b):
input = np.array([a,b])
*가중치 설정
weights = np.array([0.4,0.4])
bias = -0.6 *출력값
value = np.sum(input * weights) + bias---> 여기까지 뉴럴 한 개의 프로그램을 짠 것!!
if value <= 0:
return 0
else:
return 1
print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))x1 = np.arange(-2,2, 0.01)
x2 = np.arange(-2,2, 0.01)
bias = -0.6
y = (-0.4 * x1 - bias) / 0.4
plt.plot(x1, y, 'r--')
plt.scatter(0,0, color='orange', marker='o', s=150)
plt.scatter(0,1, color='orange', marker='o', s=150)
plt.scatter(1,0, color='orange', marker='o', s=150)
plt.scatter(1,1, color='orange', marker='^', s=150)
plt.xlim(-0.5,1.5)
plt.ylim(-0.5,1.5)
plt.grid()>>

- OR 게이트
def OR(a, b):
input = np.array([a,b])
*가중치 설정
weights = np.array([0.4,0.4])
bias = -0.3
*출력값
value = np.sum(input * weights) + bias---> 여기까지 뉴럴 한 개의 프로그램을 짠 것!!
if value <= 0:
return 0
else:
return 1
print(OR(0,0))
print(OR(0,1))
print(OR(1,0))
print(OR(1,1))- NAND 게이트
def NAND(a, b):
input = np.array([a,b]) weights = np.array([-0.6,-0.6])
bias = 0.7 value = np.sum(input * weights) + bias if value <= 0:
return 0
else:
return 1
print(NAND(0,0))
print(NAND(0,1))
print(NAND(1,0))
print(NAND(1,1))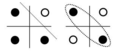
- XOR 게이트
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
print(XOR(0,0))
print(XOR(0,1))
print(XOR(1,0))
print(XOR(1,1))>>
0
1
1
0
풀려는 문제에 따라 신경망의 형태가 바뀐다.
이전의 값들이 영향을 미치는 것은 순환 신경망(Recurrent Neural Network, RNN)을 사용하는 것이 좋다.
합성곱 신경망(Convolutional Neural Network, CNN)은 필요한 특징을 잡아낼 때 사용한다.


------> 특징을 잡아 정보량을 줄여 나간다.
활성화 함수(Activation Function)는 입력 신호의 총합을 출력 신호로 변환하는 함수이다. 단층/다층 퍼셉트론을 모두 사용한다.
다음은 대표적인 활성화 함수이다.
- Sigmoid
- ReLU
- tanh
- Identity Function
- Softmax
파이썬 코드로 구현하기
1. 계단 함수(Step Function)
def step_function(x):
if x > 0:
return 1
else:
return 0
def step_function_for_numpy(x):
y = x > 0
value = y.astype(np.int)
return value
print(step_function(-3))
print(step_function(5))>>
0
1

2. 시그모이드 함수(Sigmoid Function)
: 주로 이진분류 문제에서 사용. 출력값이 0~1의 값으로 나오며 확률로 표현 가능하다. np.exp(-x)는 지수 함수
def sigmoid(x):
value = 1 / (1 + np.exp(-x))
return value
print(sigmoid(3))
print(sigmoid(-3))>>
0.9525741268224334
0.04742587317756678
plt.grid()
x = np.arange(-5,5,0.01)
y1 = sigmoid(x)
y2 = step_function_for_numpy(x)
plt.plot(x, y1,'r-')
plt.plot(x, y2, 'b--')
3. 렐루 함수(ReLu)
: 0보다 크면 그대로 출력. (0 아래로 살짝 내려가는 LeakyReLu도 있다.)
def ReLu(x):
if x > 0:
return X
else:
return 0
4. 항등 함수(Identity Function)
def identity_function(x):
return x
5. 소프트맥스 함수(Softmax)
: 소프트맥스는 세 개 이상으로 분류하는 다중 클래스 분류에서 사용되는 활성화 함수. 분류할 클래스가 n개이면 n차원의 벡터를 입력받아 확률을 추정한다.
def Softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
a = np.array([0.3,0.2,3.0,-1.2])
print(Softmax(a))
print(np.sum(Softmax(a)))>>
[0.0587969 0.05320164 0.8748821 0.01311936]
1.0
---> 소프트맥스 함수는 overflow(컴퓨터가 표현할 수 있는 숫자의 범위를 넘어서는 현상)문제로 위의 수식에서 약간 수정되어 사용된다.
softmax(x_i) = exp(x_i - max(x)) / (sum(exp(x_j - max(x))) for j in range(num_classes))
활성화 함수를 비선형 함수로 사용하는 이유?
- 신경망을 deep하게 하기 위해서
- 선형함수는 은닉층의 갯수가 의미가 없어짐
'MS AI School' 카테고리의 다른 글
| DAY 28 - 딥러닝 Training 과정 (0) | 2022.12.06 |
|---|---|
| DAY 27 - 딥러닝 프레임워크 Keras (0) | 2022.11.29 |
| Day 25 - 신경망 데이터(텐서, 1차원, 2차원, 3차원..) (0) | 2022.11.29 |
| DAY 24 - 신경망 기초 수학 (0) | 2022.11.26 |
| DAY 23 - 딥러닝 이론 (0) | 2022.11.26 |