728x90
지난 시간에는 Simple Linear Regression으로 모델을 만들어서 평가했다.
이번에는 다른 방법으로 학습시켜보자.
지난번 학습한 Supervised Learning 방법을 다시 살펴보자.

이번에는 다중 선형 회귀(Multiple Linear Regression)으로 Boston 집값 데이터를 가지고 모델을 만들어 보자.
여러 개의 값을 다룰 수 있다.
# 다중 선형 회귀(Multiple Linear Regression)를 사용한다.
# RM column 말고 전체 columns를 사용
mul_lr = LinearRegression()
mul_lr.fit(X_train, y_train)
# 테스트용 데이터를 가지고 예측하기
y_pred = mul_lr.predict(X_test)
print('다중 선형 회귀, R2: {:.4f}'.format(r2_score(y_test, y_pred)))
>> 다중 선형 회귀, R2: 0.6226
62.26%
----> 단순 선형 회귀에 비해 3배 정도 향상되었다. 그러나 여전히 정확도가 떨어진다.
이번에는 결정 트리 모델(Decision Tree Regressior)을 사용하여 RM(방의 개수) 하나의 column만을 가지고 모델을 만들어 보자.
# 결정 트리 모델(Decision Tree Regressor)- 단순 결정 트리 회귀를 사용한다.
from sklearn.tree import DecisionTreeRegressor
# max_depth: 몇 단계까지 내려갈 것인지 지정
dt_regr =DecisionTreeRegressor(max_depth=2)
# 2차원 배열로 바꾸고, 학습시키기
dt_regr.fit(X_train['RM'].values.reshape((-1,1)), y_train)
# 결과 테스트 해 보기
y_pred = dt_regr.predict(X_test['RM'].values.reshape(-1,1))
# 테스트용 데이터를 가지고 실질적으로 확인해 보자.
# R2(R Squared, R^2, 결정계수)로 원본 라벨 데이터(y_test)와 예측값(y_pred) 차이 비교하기
print('단순 결정 트리 회귀 R2: {:.4f}'.format(r2_score(y_test, y_pred)))
>>단순 결정 트리 회귀 R2: 0.3547 # 35.47%
---> max_depth에 변화를 줘 본다. 너무 높이면 학습 데이터와 오버피팅되어 테스트용 데이터와 격차가 벌어지게 된다.
반복문을 써서 가장 좋은 depth를 쓴다.
# 가장 좋은 depth를 찾기 위한 배열 만들기. 1부터 10까지
arr = np.arange(1,11)
print(arr)
>>[ 1 2 3 4 5 6 7 8 9 10]
# 가장 좋은 depth 찾기
best_depth = 1
best_r2 = 0
for depth in arr:
dt_regr = DecisionTreeRegressor(max_depth=depth)
dt_regr.fit(X_train['RM'].values.reshape((-1,1)), y_train)
y_pred = dt_regr.predict(X_test['RM'].values.reshape(-1,1))
temp_r2 = r2_score(y_test, y_pred)
print('\n단순 결정 트리 회귀 depth={} R2: {:.4f}'.format(depth, temp_r2))
if best_r2 < temp_r2:
best_depth = depth
best_r2 = temp_r2
print('최적의 결과는 depth={} r2={:.4f}'.format(best_depth, best_r2))
>>

단순 결정 트리 회귀를 사용해 보니 39.31%의 정확도가 나왔다.
이번에는 다중 결정 트리 회귀를 사용하여 전체 columns를 가지고 모델을 만들어 보자.
# 결정 트리 모델(Decision Tree Regressor)- 다중 결정 트리 회귀를 사용한다.
dt_regr = DecisionTreeRegressor(max_depth=8)
dt_regr.fit(X_train, y_train)
y_pred = dt_regr.predict(X_test)
print('다중 결정 트리 R2: {:.4f}'.format(r2_score(y_test, y_pred)))
>> 다중 결정 트리 R2: 0.740274.02%의 정확도가 나왔다.
이번에는 Support Vector Machine Regressor를 사용하여 RM(방의 개수) column만을 가지고 모델을 만들어 보자.
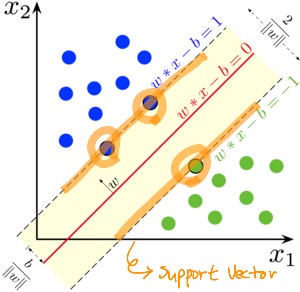
선에 걸리는 것들 = Support Vector
서포트 벡터 사이에 몇 개까지 예외로 허용할 것인지?
C=1이면 1개가 있어도 영향 받지 않고 예쁘게 선을 긋겠다!
C=2이면 2개가 있어도 영향 받지 않고 예쁘게 선을 긋겠다!
*default 값은 1
# Support Vector Machine Regressor(서포트 벡터 머신 회귀)를 사용해 보자.
from sklearn.svm import SVR
svm_regr = SVR(C=1)
svm_regr.fit(X_train['RM'].values.reshape(-1,1), y_train)
y_pred = svm_regr.predict(X_test['RM'].values.reshape(-1,1))
print('단순 서포트 벡터 머신 회귀 R2: {:.4f}'.format(r2_score(y_test,y_pred)))
>> 단순 서포트 벡터 머신 회귀 R2: 0.3763
37.63%의 정확도가 나왔다.
#결과를 시각화 해 보자.
line_X = np.linspace(np.min(X_test['RM']), np.max(X_test['RM']), 100)
line_y = svm_regr.predict(line_X.reshape(-1,1))
plt.scatter(X_test['RM'], y_test, c='black')
plt.plot(line_X, line_y, c='red')
plt.legend(['Regression line', 'Test data sample'], loc='upper left')>>
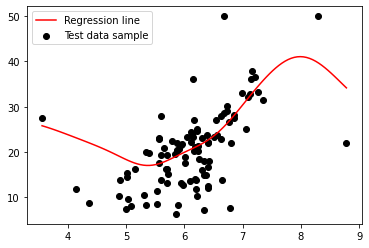
# 전체 columns, C=20으로 해 보자.
svm_regr = SVR(C=20)
svm_regr.fit(X_train, y_train)
y_pred = svm_regr.predict(X_test)
print('다중 서포트 벡터 머신 회귀, R2 : {:.4f}'.format(r2_score(y_test, y_pred)))
>>다중 서포트 벡터 머신 회귀, R2 : 0.4234
42.34%의 정확도가 나왔다.
# 반복문을 사용하여 최적의 C 값을 찾는다.
arr = np.arange(10000,25000)
arr
best_C = 0
best_r2 = 0
for C in arr:
svm_regr = SVR(C=C)
svm_regr.fit(X_train, y_train)
y_pred = svm_regr.predict(X_test)
#print('다중 서포트 벡터 머신 회귀, R2 : {:.4f}'.format(r2_score(y_test, y_pred)))
if best_r2 < temp_r2:
best_depth = depth
best_r2 = temp_r2
print('최적의 결과는 depth={} r2={:.4f}'.format(best_depth, best_r2))
이번에는 Multi Layer Perceptron Regressor를 사용하여 Boston 집값 데이터(전체 columns)를 가지고 모델을 만들어 보자.
- 멀티레이어 퍼셉트론?
- 퍼셉트론을 여러층 쌓은 순방향의 인공 신경망
- 복잡한 문제를 대략적으로 해결할 수 있도록 확률적으로 문제를 해결하는 능력
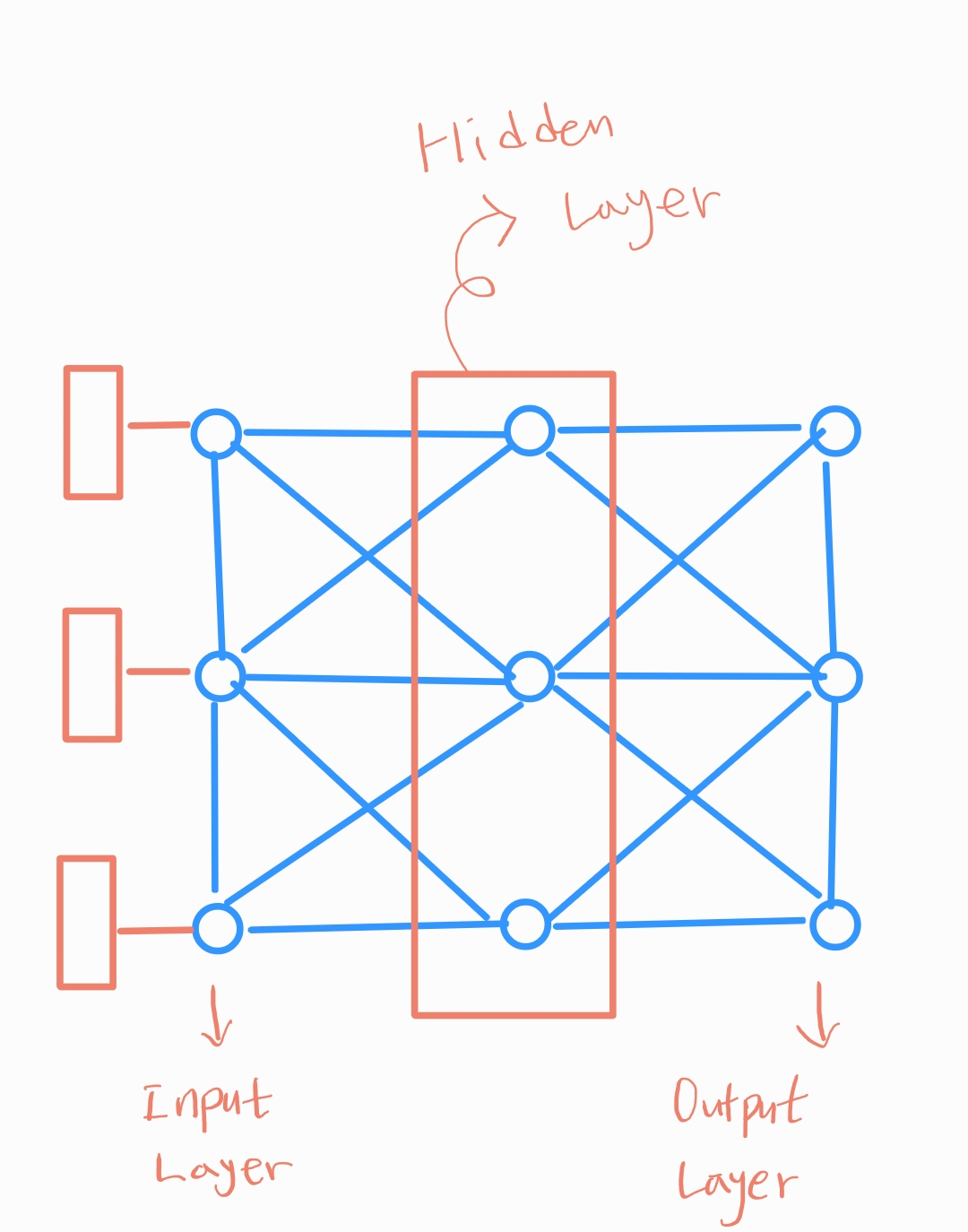
# 파라미터 주기. parameter solver 종류: lbfgs, sgd, adam
from sklearn.neural_network import MLPRegressor
mlp_regr = MLPRegressor(solver='adam',hidden_layer_sizes=100)
# 학습시키기
mlp_regr.fit(X_train, y_train)
# 결과 테스트 해 보기
y_pred = mlp_regr.predict(X_test)
print('다중 MLP 회귀, R2: {:.4f}'.format(r2_score(y_test,y_pred)))
>> 다중 MLP 회귀, R2: 0.3909
# 39.09%인 다중 레이어 퍼셉트론 모델을 만들었다.
# max_iter를 추가해 보자. 최대 반복 횟수 지정하는 것
from sklearn.neural_network import MLPRegressor
mlp_regr = MLPRegressor(solver='adam',hidden_layer_sizes=100,max_iter=1000)
# 여기까지 멀티레이어 퍼셉트론 준비 완료
# 학습시키기
mlp_regr.fit(X_train, y_train)
# 결과 테스트 해 보기
y_pred = mlp_regr.predict(X_test)
print('다중 MLP 회귀, R2: {:.4f}'.format(r2_score(y_test,y_pred)))
>> 다중 MLP 회귀, R2: 0.456945.69%인 다중 레이어 퍼셉트론 모델을 만들었다.
728x90
'MS AI School' 카테고리의 다른 글
| DAY 22 - 머신러닝 비지도 학습: 클러스터링(Clustering) (0) | 2022.11.23 |
|---|---|
| DAY 21 - 머신러닝 지도 학습: 분류(Classification) (0) | 2022.11.23 |
| DAY 19 - 머신러닝 지도 학습: 선형 회귀 (0) | 2022.11.01 |
| DAY 18 - Scikit Learn 머신러닝 모델 만들기 (0) | 2022.11.01 |
| DAY 15 - Feature와 Label, Data Preprocessing(데이터 전처리) (0) | 2022.11.01 |